Criando problemas matemáticos para os anos iniciais

Janaína Mota Fidelis

Pense comigo: para saber matemática, basta somente saber calcular? A aprendizagem matemática, além da capacidade de cálculo, está relacionada à compreensão contextual para buscar a resposta adequada (SANTOS; FERNANDES, 2016).

Nesse sentido, o raciocínio quantitativo pode ajudar a decidir qual é o melhor cálculo para resolver determinada situação, ou mesmo, utilizar outros mecanismos menos “escolarizados” para encontrar um resultado lógico e correto (NUNES; DORNELES; LIN; RATHGEB-SCHNIERER, 2016; NUNES; CARRAHER; SCHLIEMANN, 2011).

Por que estou dizendo isso? Porque o trabalho pedagógico através de resolução de problemas significativos, pode auxiliar no desenvolvimento de diversas habilidades matemáticas, entre elas a do raciocínio quantitativo.

Nesse curso você irá embarcar na aventura de refletir e depois poderá levar os seus estudantes a refletirem sobre a análise, criação e resolução de problemas matemáticos.

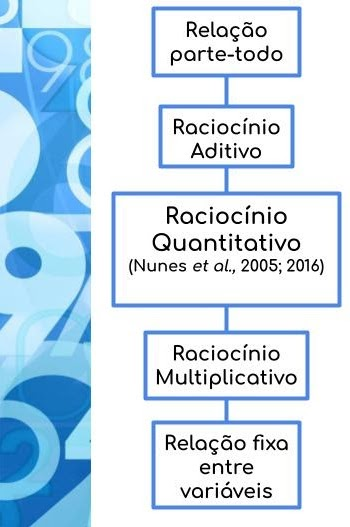
Durante o curso, você poderá compreender as diferenças entre raciocínio aritmético e raciocínio quantitativo, refletindo sobre a importância dessa diferenciação para uma abordagem significativa da resolução de problemas matemáticos. Será possível refletir sobre esses temas através de exemplos práticos.

O passo seguinte será aprofundar as discussões sobre os tipos de raciocínio quantitativo e como eles se apresentam nas diferentes situações-problema. Toda a reflexão e os exemplos de problemas envolvendo o campo aditivo e o multiplicativo serão pensados com base na BNCC, através de exemplos práticos do cotidiano escolar.

Através da resolução de problemas é possível criar uma ponte entre o conteúdo escolar e a vida cotidiana (VERSCHAFFEL et al., 2000), de maneira desafia o estudante a pensar matematicamente sobre a tarefa, permitindo que a matemática faça sentido (ONUCHIC; ALLEVATO, 2011). Contudo, muitas vezes a maneira como o problema é trabalhado, faz com que se pense sobre eles de maneira superficial (VAN DOOREN et al., 2019).

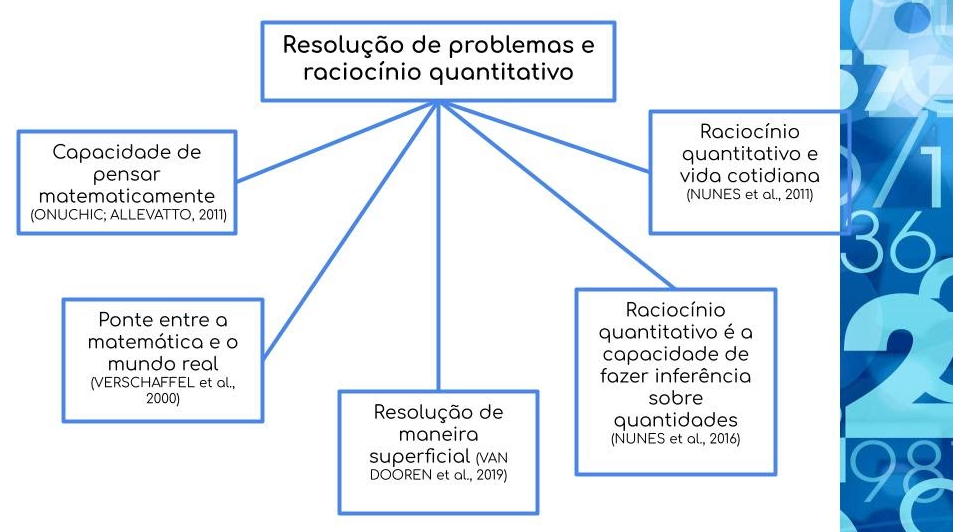
Por isso, trabalhar a resolução de problemas pautada no raciocínio quantitativo, favorece o desenvolvimento da capacidade de fazer inferências sobre quantidades (NUNES et al., 2016). Essa capacidade, muitas vezes bem desenvolvida na vida cotidiana de trabalhadores, pode ser pensada na matemática escolar (NUNES et al., 2011).

Nos acompanhe nesse curso para ver na prática como é possível criar suas próprias situações-problema para dar significado às suas aulas de matemática, ou ainda, fazer com que os estudantes pensem matematicamente e criem situações-problema para seus pares resolverem. Essa é uma boa proposta para que o ensino e a aprendizagem da matemática ocorram de maneira reflexiva e eficaz!

Referências:

NUNES, T.; CAMPOS, T. M. M.; MAGINA, S.; BRYANT, P. Educação matemática: Números e operações numéricas. São Paulo: Cortez, 2005.

NUNES, T.; CARRAHER, D.; SCHLIEMANN, A. Na vida dez, na escola zero. 16 º ed. São Paulo: Cortez, 2011.

NUNES, T.; DORNELES, B. V.; LIN, P. J.; RATHGEB-SCHNIERER, E.. Teaching and Learning About Whole Numbers in Primary School. In: ICME-13 Topical Surveys. Springer O ed. Hamburg, 2016.

ONUCHIC, L. R.; ALLEVATO, N. S. G. Pesquisa em Resolução de Problemas: caminhos, avanços e novas perspectivas. In: Bolema, v. 25, n. 41, p. 73 – 98, 2011.

SANTOS, A. A. A.; FERNANDES, E. S. O. Habilidade de Escrita e compreensão de leitura como preditores do desempenho escolar. Psicologia Escolar e Educacional, SP. v. 20, n. 3, p. 464 – 473, set./ dez. 2016.

VAN DOOREN, V.; LEM, S.; DE WORTELAER, H.; VERCHAFFEL, L. Improving realistic word problem solving by using humor. In: Journal of Mathematical Behavior. V.53, p. 96 – 104, mar. 2019.

VERSCHAFFEL, L.; GREER, B.; DE CORTE, E. Making sense of word problems. Lisse, Nederland: Swets & Zeitlinger, 2000.